Ooit wel eens van het ‘grootvaderparadox’ gehoord?

Het gaat als volgt: stel dat ik terug in de tijd zou reizen en daarbij mijn grootvader zou vermoorden (of in ieder geval zorgen dat hij mijn grootmoeder niet zou ontmoeten) voordat mijn ouders geboren zijn, hoe kan ik dan nu nog bestaan?

In de kwantummechanica hoeft dit geen paradox te zijn, omdat er ‘simpelweg’ in verschillende parallelle universa gereisd kan worden. In dat geval zou ik in één van die universa wel bestaan, maar mijzelf in een ander parallel universum uitgeschakeld hebben.

Stephen Hawking verwacht dat tijdreizen in de toekomst mogelijk zal gaan worden. Echter, gaat hij ervan uit dat er alleen naar de toekomst gegaan kan worden en niet naar het verleden. Zijn onderbouwing voor het laatste is dat er bij tijdreizen naar het verleden paradoxen zullen ontstaan waardoor het simpelweg onmogelijk is (net zoals het bovengenoemde grootvaderparadox).

Een tijd terug zat ik te fantaseren over oneindigheid en bedacht ik hier een aantal eigenschappen bij. Ineens stuitte ik op een eigenschap waarmee ik Hawking’s vermoeden, dat terug in de tijdreizen niet mogelijk is, op een wiskundige manier aan denk te kunnen tonen.

Ik neem jullie nu mee in mijn gedachte experiment.

1. Stel je hebt een object A waarvan de afmetingen in alle drie de dimensies eindig zijn (in de wereld waarin wij leven is dit voor elk object het geval), beweging binnen alle drie de dimensies (x, y en z) is dan mogelijk (zie figuur 1).

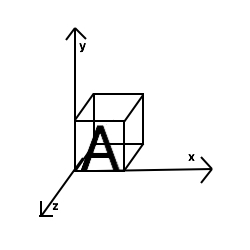
Figuur 1: eindig x eindig x eindig

2. Stel nu dat A in alle drie de dimensies (‘volledig’,hiervan volgt de uitleg) oneindig is, dan kan A zich niet meer bewegen. Immers, A is reeds overal en er zijn dus geen punten meer om naartoe te bewegen. Een voorbeeld van een dergelijk ‘object’ is het universum.

3. Laat A nu in dimensie z (volledig) oneindig zijn en in dimensie x en y wel eindig zijn. Beweging binnen dimensie z is nu niet meer mogelijk, immers A is al overal binnen deze dimensie. Maar beweging binnen dimensie x en y is nog wel mogelijk, want hier zijn punten waar A nog niet is (zie figuur 2).

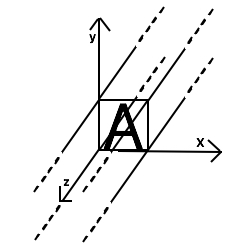
Figuur 2: eindig x eindig x (volledig) oneindig

4. Stel nu dat A binnen dimensie x en y nog steeds eindig is, maar nu binnen dimensie z ‘eindig-oneindig’. Oftewel: binnen één richting van dimensie z gaat A oneindig lang door, maar de andere kant op is A wel eindig (zie figuur 3).

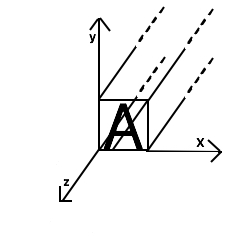
Figuur 3: eindig x eindig x eindig-oneindig

Bij deze laatste stap kan A zich nu wel binnen dimensie z bewegen, maar slechts in één richting. In de richting waarin A eindig is, is beweging nog mogelijk. Tegelijkertijd is beweging, in de richting waarin A oneindig is, niet mogelijk, aangezien het daar overal al is.

Terug naar het fenomeen tijdreizen.

Tijd is in de richting van het verleden toe oneindig lang; er is geen begin van de tijd. Tegelijkertijd beweegt tijd zich richting de toekomst, maar is het daar nog niet. In de richting van de toekomst is tijd dus eindig. Tijd heeft dus dezelfde eigenschappen als de laatste stap van object A. Vanwege deze eigenschappen kan tijd maar één richting op bewegen en dat is richting de toekomst.

Conclusie: Het ontmoeten van je betovergrootouders behoort dus helaas niet meer tot de mogelijkheden. Maar het ontmoeten van de kinderen van je kleinkinderen, je toekomstige geliefde of de wereldkampioen voetbal in het jaar 2478 is nog niet uitgesloten.

*Voor de oplettende lezer: voor tijd is slechts één dimensie relevant. Hiermee heeft het de eigenschappen van A slechts over dimensie z. De dimensies x en y kunnen als niet aanwezig beschouwd worden of de afmetingen hiervan kunnen beiden als (volledig) oneindig beschouwd worden. Het gebruik van deze andere twee dimensies waren slechts ter verheldering van mijn argumentatie.