Een hotel met oneindig veel kamers. Het is wat groot en moeilijk voor te stellen, maar dit hotel vormde de basis van de kritiek op de tijd-reis-theorie die ik bijna een half jaar geleden schreef. In die blog beargumenteerde ik dat terug in de tijd reizen niet mogelijk zou zijn. De strekking van mijn theorie lag bij de bewegingseigenschappen van objecten met een oneindige afmeting. Namelijk dat er in de richting van de oneindigheid geen beweging mogelijk is, aangezien elk punt in die richting al bereikt is. Nadat ik mijn theorie aan een paar wiskundigen/natuurkundigen voorgelegd heb, ontving ik van de meesten een kritiek van vergelijkbare aard. Beweging in de richting van oneindigheid is wel degelijk mogelijk. Hun onderbouwing hiervoor is het gedachte-experiment van Hilbert’s Hotel, een theorie van een invloedrijke wiskundigen van de negentiende en begin twintigste eeuw: David Hllbert. Omdat deze beweging wel mogelijk is, leek mijn theorie aan slagkracht te verliezen.

Daar zat ik dan, overtuigd van mijn eigen theorie, maar tegelijkertijd instemmend met de ontvangen feedback.

Toen bedacht ik mij dat beide theorieën elkaar niet hoeven uit te sluiten. In deze blog zal ik uitleggen waarom dit niet hoeft. Om dit te kunnen doen is het eerst goed om te begrijpen wat het gedachte-experiment van Hilbert’s Hotel precies inhoudt.

Hilbert’s Hotel

Het hotel van Hilbert is een hotel met oneindig veel kamers, elk met een eigen (positief) nummer (1, 2, 3, … ). Op een gegeven moment zit het hotel helemaal vol. Diezelfde dag komt er een reiziger aan bij de receptie die niet heeft gereserveerd. In elke hotel met een eindig aantal kamers zou deze toerist pech gehad hebben en door moeten zoeken naar een ander hotel of op straat moeten slapen. Maar in Hilbert’s Hotel is dat niet het geval. De manager vraagt aan de persoon in kamer 1 te verplaatsen naar kamer 2, de persoon in kamer 2 te verkassen naar kamer 3, enzovoort. De persoon in kamer n gaat dus naar kamer n+1. Hierdoor kan de toerist nu in kamer 1 terecht. In een hotel met een eindig aantal kamers zou dit geen optie geweest zijn, omdat de gast met het hoogste kamernummer nergens heen zou kunnen. In Hilbert’s Hotel is er echter geen gast met hoogste kamernummer en is dit wel mogelijk.

Opgelucht dat de toerist toch een kamer heeft kunnen krijgen, ziet de manager vervolgens een bus vol toeristen aan komen rijden. Dit is een erg bijzondere bus, want er zitten oneindig veel reizigers in. Even schiet bij de manager het zweet op zijn voorhoofd, hetzelfde trucje van net zal namelijk niet meer werken. Zelfs als elke gast een miljoen kamers zal moeten verschuiven, zal dit evengoed te weinig zijn om een oneindig aantal nieuwe gasten een bed aan te bieden.Dan bedenkt hij een oplossing. Hij vraagt de gast uit kamer 1 te verplaatsen naar kamer 2, de gast uit kamer 2 naar kamer 4 te gaan, 3 naar 6, enzovoort. Elke persoon in kamer n zal nu dus naar kamer 2n gaan en zodoende komen alle oneven kamers vrij. Vervolgens zal hij de reiziger met busplek 1 kamer 1 toewijzen, de reiziger met busplek 2, kamer 3 enzovoort. Elke reiziger met busplek n zal in het hotel kamer 2n – 1 toegewezen krijgen. Op die manier kunnen oneindig veel gasten dus zelfs nog een kamer krijgen in het aanvankelijk volle hotel.

In het gedachte-experiment van Hilbert’s Hotel komen er even later zelfs oneindig veel bussen aanrijden met oneindig veel reiziger en weet de manager hen zelfs allemaal een kamer toe te wijzen in het hotel. Deze laatste stap is echter niet meer relevant voor mijn theorie, dus de wijze waarop hij dit doet mag u als lezer zelf uitvogelen.

Discussie

In het voorbeeld van Hilbert’s Hotel blijkt dat beweging in de richting van oneindigheid wel mogelijk is aangezien elke gast een andere (hogere) kamer toegewezen kan krijgen. Om duidelijk te maken dat deze twee theorieën niet in tegenspraak zijn met elkaar, maak ik graag onderscheid tussen twee verschillende vormen van beweging (en ken hier twee woorden aan toe die niet perse gangbaar zijn in deze context): ‘Intrinsieke beweging’ en ‘Extrinsieke beweging’.

1. Intrinsieke beweging: bij intrinsieke beweging vindt de beweging slechts plaats op het reeds ‘bezette’ gebied. In andere woorden: binnen een object is er beweging mogelijk, maar het object als geheel verandert niet van locatie. Ter illustratie onderstaande afbeelding (afbeelding 1). Hierin is er beweging mogelijk van kamer 1, naar kamer 2, van 2 naar 3, enzovoort. Echter blijft het object als geheel op dezelfde plek en beweegt zich zodoende niet.

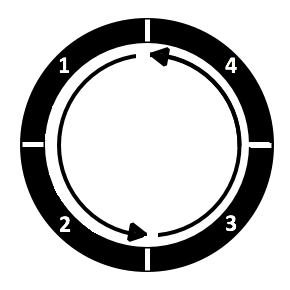
Afbeelding 1: Intrinsieke beweging

2. Extrinsieke beweging: hier is sprake van wanneer een object als geheel  van plek A naar plek B beweegt (waarbij A niet gelijk is aan B). Dit wordt in onderstaande afbeelding (afbeelding 2) getoond.

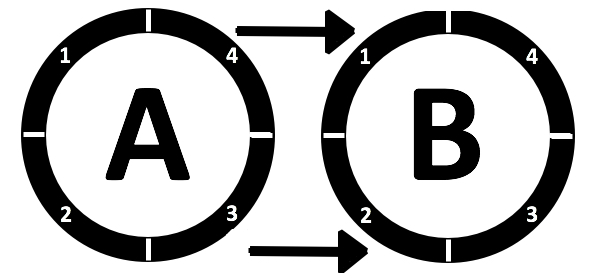
Afbeelding 2: Extrinsieke beweging 

In Hilbert’s Hotel is er duidelijk sprake van intrinsieke beweging. Het totaal aantal kamers verandert niet, er wordt alleen binnen de kamers van het hotel geschoven, terwijl in mijn theorie de extrinsieke vorm aangehaald wordt omdat de beweging van het object als geheel de basis van de argumentatie vormt.

Intrinsieke- en extrinsieke beweging sluiten elkaar niet uit en het aanwezig zijn van de één, zegt niks over het al dan wel of niet mogelijk zijn van de ander. Dit betekent dat Hilbert’s Hotel slechts aantoont dat intrinsieke beweging mogelijk is in de richting van oneindigheid, maar zegt tegelijkertijd niks over de mogelijkheden van extrinsieke beweging. Hiermee is het ongelijk van mijn theorie dus niet bewezen.

In de hoop dat deze blog voor de nodige intrinsieke beweging in de bovenkamer van u als lezer zal zorgen. Ga ik diezelfde intrinsieke beweging nu verminderen door mij met extrinsieke beweging naar mijn bed te begeven. Salut.